Les matrices de probabilités

Qu’est ce qu’une matrice de probabilités ?
La difficulté dans tout type de pari hippique est de déterminer la probabilité qu’un pari se réalise. C’est même le cœur du sujet, car si on pouvait déterminer avec exactitude la probabilité qu’un pari soit gagnant, alors il suffirait de jouer selon ces probabilités, lorsque l’espérance de gain est positive, pour être gagnant à terme.
Seulement, déterminer ces probabilités avec exactitude est impossible, sauf à considérer tous les chevaux réellement égaux au départ, ce qui n’est pas réellement le cas, et c’est ce qui fait justement l’intérêt des paris hippiques par rapport à d’autres jeux de pur hasard: c’est parce que les probabilités de réussite de chaque cheval ne sont pas égales, qu’on peut espérer réduire la part de hasard et augmenter son espérance de gain, en déterminant le mieux possible ces probabilités, à travers différents moyens. Le PMU étant un jeu reposant sur le principe du pari mutuel, ce sont les parieurs disposant des meilleurs outils qui prendront l’avantage sur les autres, et auront le plus de chances de gagner sur une stratégie moyen/long terme.
La matrice de probabilités est un de ces outils.
Je parle ici de matrice car pour construire la meilleure stratégie de pari, il faut prendre en compte un maximum d’informations, et pas seulement la probabilité qu’un cheval gagne ou pas. Le fait qu’un cheval ait également certaines chances d’être 2ème , 3ème, 4ème ou 5ème est aussi une information importante lorsqu’on souhaite construire une stratégie de jeu en couplé, tiercé, quarte, quinte, multi.. D’ailleurs on retrouve souvent dans la presse hippique des commentaires type « pour une 4ème ou 5ème place » ou alors « à ne pas écarter », signe qu’un cheval n’est pas jugé suffisamment bon pour être dans les tous premiers , mais qu’il a quand même ses chances d’être dans l’arrivée et devrait donc être pris en considération dans l’établissement des paris pour un quarté ou un quinté par exemple.
Une matrice de probabilités représente donc pour chaque cheval et chaque place à prendre en compte dans le pari joué, la probabilité que le cheval arrive à cette place.
Voici un exemple de matrice de probabilités pour un quinté à 15 partants:

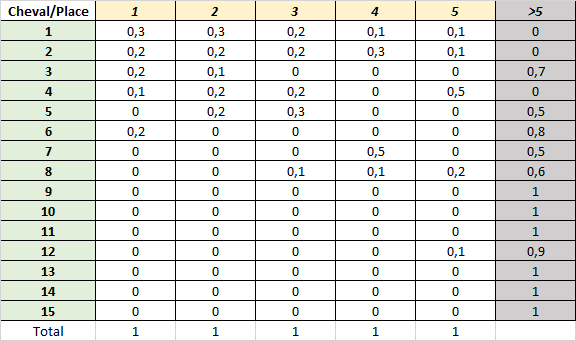
Pour chacune des 5 places de l’arrivée, chaque probabilité doit être comprise entre 0 et 1 et la somme des probabilités doit être égale à 1, puisqu’un et un seul cheval va arriver à cette place.
Pour chaque cheval, la probabilité qu’il arrive dans une place après la 5ème place (ces places sont regroupées dans une seule catégorie « >5 », qui inclut également les chevaux disqualifiés et tombés) est donc égale à 1- somme des probabilités d’arriver dans les 5 premières places. Cette probabilité « >5 » doit donc être comprise entre 0 et 1.
Ce sont les seules contraintes de cette matrice pour qu’elle soit valide mathématiquement. Ensuite, des règles de bon sens peuvent aider à vérifier la pertinence d’une matrice. Par exemple, il serait étrange qu’un cheval ait une probabilité positive d’être 1er et 5ème, mais que sa probabilité d’être 2ème, 3ème ou 4ème soit nulle.

Comment créer une matrice de probabilités ?
Nous allons ici nous attacher à présenter 5 façons différentes de créer ces matrices. Les déclinaisons possibles de ces 5 types sont ensuite infinies, l’important est de comprendre le principe de construction.

1/Matrice par cote
On considère dans cette méthode que les parieurs ont raison. C’est-à-dire que les cotes, qui sont déterminées par les enjeux des parieurs (et donc par la somme de leurs estimations personnelles des probabilités de gain), reflètent directement les probabilités réelles de gain des chevaux.
Pour illustrer cela je vous invite à lire l’article Enjeux, cotes, rapports et TRJ: comment sont-ils liés?
On voit dans l’exemple détaillé dans cet article, qu’il est possible de calculer les enjeux en pourcentage pour chaque cheval, à partir des rapports probables (on utilisera les rapports probables à 10min, afin d’avoir le temps de faire tourner les algorithmes et de placer les paris).
Comme je l’explique dans l’article , on calcule tout d’abord le TRJ probable en appliquant la formule suivante:

   

où Ri est le rapport probable du cheval numéro i.
Cela permet ensuite de calculer pour chaque cheval les enjeux (en pourcentage de l’enjeu total), à l’aide de la formule suivante, également démontrée dans l’article cité ci-dessus :

   

On obtient ainsi les enjeux en pourcentage, pour chaque cheval:

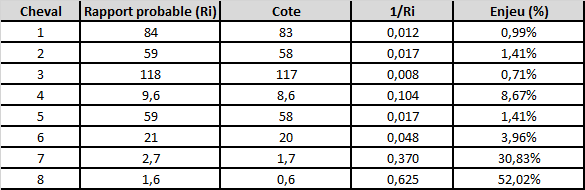
Si on considère que les probabilités sont proportionnelles aux enjeux, le tableau ci-dessus fournit donc également les probabilités de victoire de chaque cheval pour la course citée en exemple, selon cette méthode.
Mais comment passer de cette matrice de probabilité de victoire, à une matrice de probabilités pour chaque place, telle que celle pour le quinté, dont un exemple est donné ci-dessus ?
En d’autres termes, comment déterminer les probabilités d’arrivée à une place donnée, lorsqu’on a seulement la probabilité d’arrivée à la première place ?
Des règles (hypothèses) doivent à ce stade être prises comme par exemple : si un cheval est ultra favori (rapport inférieur à X, ou encore probabilité de victoire supérieure à Y% par exemple, avec X et Y à définir), alors on peut considérer qu’il a également une probabilité inférieure mais toujours importante d’être 2ème, puis d’être 3ème etc.. On peut ainsi appliquer un pourcentage dégressif par rapport à la probabilité de départ. Ce pourcentage pourrait même varier selon des tranches de probabilité de victoire, à définir. Les contraintes de somme présentées dans l’exemple de matrice ci-dessus doivent également être prises en compte.
Vous pouvez aussi vous inspirer de la méthode d’Harville, qui a travaillé sur cette question.

2/Matrice par pronostics
L’idée ici est de ne pas utiliser les cotes, mais plutôt des pronostics, qui peuvent provenir de diverses sources. En effet la méthode par les cotes, présentée précédemment, a a priori l’inconvénient de s’appuyer sur l’opinion générale des parieurs et donc de fournir des gains modérés lorsqu’elle est gagnante, puisque les gains devront être partagés avec l’ensemble des parieurs.
Ceci est bien entendu à nuancer, puisque la méthode par cote intègre des règles de répartition propres comme expliqué ci-dessus, et que la matrice de probabilités n’est qu’un élément de la stratégie de jeu, qui comprend d’autres éléments comme la sélection des courses, la détermination des mises, la génération des combinaisons à l’aide par exemple de systèmes réducteurs, ou encore l’optimisation du taux de couverture, en jouant plusieurs types de paris, permettant de recouvrir différents scenarios et d’assurer des gains minimum dans un maximum de cas.
Mais revenons à la méthode par pronostics.
L’idée ici est de récolter un maximum d’informations de diverses sources: presse hippique classique, certains sites internet de pronostics, informations fournies par Equidia en live, connaissances dans le milieu hippique… toute information est bonne à prendre, pour peu qu’on ait un minimum confiance en la source, et qu’on recoupe les informations (tout pronostiqueur, même le meilleur, n’a jamais tout le temps raison !).
Un exemple simple est le tableau de citations dans la presse, qu’on peut retrouver dans différentes sources d’information hippiques : à chaque fois qu’un cheval est cité dans un pronostic en places 1,2,3 etc..jusqu’à 8 en général, on lui attribue un point. On a ainsi un nombre de points/citations pour chaque cheval, à chaque place.
Voici un exemple avec un tableau de citations trouvé dans la presse pour le quinte du 22 Avril 2019 :

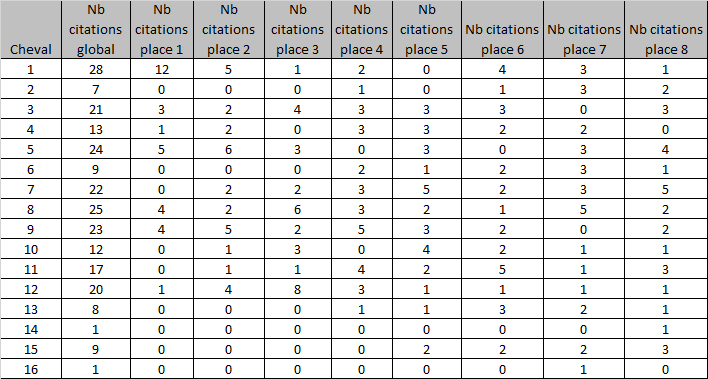
On peut alors à partir de ce tableau, construire une matrice de probabilités.
Par exemple, en faisant le rapport, pour chaque place de 1 à 5, du nombre de citations du cheval, par le nombre de citations de l’ensemble des chevaux. Ici le cheval 1 cité 12 fois en place 1, a donc une probabilité de 12/30 (l’ensemble des chevaux étant cité 30 fois en place 1). On obtient ainsi cette matrice :

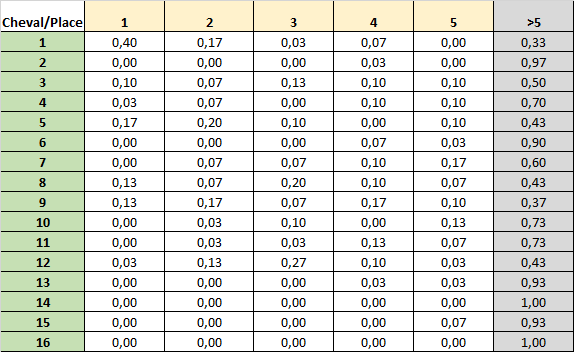
Bien entendu vous pouvez définir vos propres règles de calcul pour déterminer les probabilités à partir du nombre de points.

3/Matrice par score ou combinaison de critères
Cette méthode est basée sur une analyse personnelle, en exploitant par exemple une base de données propre, comme le fait Turfmining, selon des critères personnels, s’affinant avec l’expérience.
On liste l’ensemble des critères que l’on considère comme pouvant impacter les chances de chaque cheval d’être à chacune des places considérées à l’arrivée, et que l’on peut quantifier.
Par exemple : la musique du cheval, le déferrage, le numéro de corde ou la place à l’autostart, les performances récentes du jockey ou de l’entraîneur etc… les paramètres possibles sont nombreux. Vous pouvez pour établir votre propre liste, vous inspirer des analyses statiques présentées sur ce site. Si vous disposez de votre base de données, vous pouvez également définir et calculer vos propres indicateurs. Rien n’interdit bien sûr d’intégrer encore les cotes ou les pronostics en paramètres d’entrée.
Il ne reste alors plus qu’à attribuer un poids à chaque indicateur en fonction de son importance à vos yeux, pour établir un score pour chaque cheval, à chacune des places.
Comme dans la méthode précédente, on convertit alors ce score en pourcentages ou probabilités. Vous obtenez ainsi une matrice de probabilités qui vous est propre, et vous différenciera donc des autres parieurs, augmentant ainsi le gain que vous pouvez espérer en cas de victoire.

4/Matrice par historique de données (ou matrice bayésienne)
A la différence des méthodes ci-dessus, qui calculent une matrice sur la seule base des données de la course en question, l’idée ici est de déterminer une matrice correspondant à une moyenne sur un historique de données, à la manière des méthodes de reverse engineering, ou plutôt de la méthode de l’inférence bayésienne, puisqu’on parle de probabilités (c’est pourquoi je qualifie cette matrice de « matrice bayésienne »).
Par exemple, on peut calculer, à partir d’une base historique de pronostics d’un journal, les pourcentages de cas où chaque cheval cité arrive en places 1,2,3,4,5, ou >5. On peut alors en faire une matrice de probabilités. Cela signifie cependant qu’on suppose que la course à venir va suivre la distribution passée des pronostics du journal. Il se peut évidemment que ce ne soit pas le cas. Mais sur un périmètre plus précis, comme un hippodrome, un jour de la semaine, un type de course.. il est possible que des liens de performance existent réellement et qu’on puisse identifier un modèle plus ou moins reproductible.
Un autre exemple serait lié aux cotes. Si l’analyse mathématique nous permet de valider que sur un périmètre précis de courses, la distribution des arrivées suit un modèle moyen reproductible et lié à la cote des chevaux, alors on peut à partir d’un historique de données sur ces courses, déterminer une matrice de probabilités en fonction de la cote des chevaux. On ne sera pas à l’abri bien sûr que la course que l’on joue soit en dehors de la moyenne, mais là encore, le fait de jouer plusieurs paris, basés sur des probabilités et non un pronostic fixe, permettra de lisser cet effet. A terme, en rejouant plusieurs fois selon cette méthode, on devrait bien se rapprocher de la moyenne et donc obtenir des paris gagnants, si le modèle est réellement globalement reproductible.
Afin d’évaluer cette reproductibilité, on pourra analyser certaines caractéristiques mathématiques de notre modèle, comme l’écart type. Le backtest nous indiquera également, en fournissant le pourcentage de cas de réussite et le gain moyen, si on est souvent proche de la moyenne (et si on peut donc considérer le modèle comme reproductible), ou bien si on s’en écarte trop souvent.

5/Matrice par machine learning
Comme nous l’évoquons ici, il est possible à l’aide de modèles de machine learning de prédire les probabilités qu’un cheval arrive en places 1,2,3,4,5, ou >5.
Cette méthode est la plus puissante a priori, et englobe en fait les différentes méthodes présentées ci-dessus, puisqu’elle va pouvoir prendre en compte les cotes, pronostics, et l’ensemble des variables que l’on veut prendre en compte, pour alimenter nos modèles de machine learning et automatiquement prédire les probabilités d’arriver à chacune des places.

Conclusion
Il existe une multitude de façons de construire une matrice de probabilités, en déclinant des variantes des 5 méthodes présentées ici, la dernière par machine learning étant a priori la plus complète et la plus pertinente.
Mais quels que soient la méthode, les paramètres et la manière dont vous les utilisez pour créer votre matrice, il est important de confronter votre matrice à la réalité afin de valider sa pertinence. Pour cela, il faudra la backtester en construisant votre matrice toujours selon les mêmes règles, et en l’appliquant au sein d’une stratégie de jeu ; en effet comme cela est expliqué dans le point 2/ de cet article, la matrice de probabilité est seulement une composante d’une stratégie globale de jeu. Vous pourrez ainsi déterminer le pourcentage de réussite de chaque méthode, mais également les gains moyens qu’elles génèrent, puis perfectionner votre méthode et votre stratégie.
A titre d’exemple, une stratégie de jeu peut être d’appliquer la matrice de probabilités à notre outil de Génération de Paris par Matrice de Probabilités.

N’hésitez pas à commenter cet article, et notamment si vous pensez avoir trouvé une méthode particulièrement intéressante pour établir une matrice pertinente.