Optimiser sa mise au quinté

Publié le par

Le quinté est certainement le pari qui fait le plus rêver les parieurs, puisque c’est celui permettant d’obtenir les plus beaux gains.
Mais c’est aussi le plus complexe, car pour obtenir le quinté ordre, il faut désigner 5 chevaux parmi l’ensemble des partants, et prévoir leur ordre d’arrivée.
A ce stade quelques notions mathématiques basiques – mais bonnes à rappeler – sont nécessaires pour évaluer la complexité de la chose:
– une permutation d’un ensemble d’éléments est une disposition ordonnée de tous les éléments de cet ensemble
– un arrangement d’un ensemble d’éléments est une disposition ordonnée d’un certain nombre d’éléments de cet ensemble
– une combinaison d’un ensemble d’éléments est une disposition non ordonnée d’un certain nombre d’éléments de cet ensemble

Dans le cadre du quinté, on ne devra ordonner que 5 chevaux parmi plus de 5 partants, la notion de permutation n’est donc pas pertinente ici (on devra pour cela attendre qu’un opérateur sorte un pari consistant à ordonner tous les chevaux de la course!)
En revanche les arrangements et combinaisons seront souvent manipulés pour calculer le nombre de paris à effectuer en fonction d’une sélection de chevaux, et du choix de vouloir jouer dans tous les ordres ou non.

Ainsi par exemple, si on souhaite jouer tous les quintés possibles (dans tous les ordres) sur une course de 16 partants (nombre moyen de partants sur les courses de quinté), le nombre de paris à jouer correspondra au nombre d’arrangements de 5 chevaux parmi 16, qu’on note A_{16}^5 ce qui revient à

    \[\frac{16!}{(16-5)!} \text{= 524 160 paris}\]

soit plus d’1 Million € d’enjeu.
Bien supérieur au rapport moyen que l’on peut désormais espérer au quinté ordre, même le dimanche avec la tirelire, car le risque est important de devoir partager le gain avec d’autres parieurs gagnants.
Et avec 20 partants le nombre de paris à jouer monte à 1 860 480.

A titre de comparaison, au loto pour gagner le jackpot il faut choisir:

  • 5 numéros parmi 49 (sans notion d’ordre, on est donc dans le cas des combinaisons, et on a 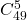C_{49}^5 soit

        \[\frac{49!}{5!(49-5)!} \text{= 1 906 884 combinaisons possibles}\]

  • puis choisir 1 « numéro Chance » parmi 10, donc 10 possibilités

Le nombre total de combinaisons possibles avec 5 bons numéros et le numéro Chance est donc de
19 068 840.

On a donc:

    \[ {\frac{19\:068\:840}{524\:160} \text{ = 36 fois plus de chances en moyenne de gagner le quinté ordre que le loto.}\]

Mais les gains potentiels ne sont pas les mêmes.
Sur les 10 dernières années, le jackpot moyen au loto est de 6,7M€ environ, alors qu’au quinté ordre, le gain moyen est de 70 000€ environ sur la même période (et 50 000€ en online).
Sur le papier l’espérance de gain du jackpot (bonus mis à part donc) quand on joue une grille de 2,2€ au loto est donc en moyenne de:

    \[ \frac{670\:0000}{19\:068\:840}-2,2*(1-\frac{1}{19\:068\:840})=-1,85 \text{ euros} \]

Alors qu’aux courses l’espérance de gain du quinté ordre (bonus mis à part) quand on joue un quinté unitaire à 2€ est en moyenne de:

    \[ \frac{70\:000}{524\:160} -2 * (1-\frac{1}{524\:160})=-1,87 \text{ euros} \]

Les espérances de gain sont donc similaires et négatives, même si elles sont un peu meilleures en réalité lorsqu’on prend en compte les bonus gagnés au loto ou au quinté pour avoir trouvé certains numéros (ou chevaux).

La différence réside surtout dans le fait que le loto repose entièrement sur le hasard, alors que ce n’est pas le cas pour les courses hippiques.
On peut considérer les combinaisons du loto équiprobables, alors que les résultats au quinté dépendent fortement des chevaux, et donc de leur cote et des pronostics.
On peut donc au quinté tirer parti de cet avantage probabiliste pour chercher à jouer un maximum de paris, mais en optimisant le coût total de ces paris par rapport à l’espérance de gain. Pour cela la seule possibilité est de restreindre le nombre de paris à jouer, en éliminant les moins probables, et en jouant au contraire un maximum de paris contenant des chevaux ayant de bonnes chances de faire l’arrivée.
C’est le principe des systèmes réducteurs, et notamment des systèmes de jeu combiné ou en champ permis par les opérateurs.
On sélectionne pour cela les chevaux en les classant en 2 catégories :

  • Les bases, ou chevaux que l’on considère comme favoris et que l’on souhaite jouer dans tous les arrangements
  • Les autres chevaux que l’on considère comme ayant des chances de faire partie de l’arrivée, qualifiés de « chevaux associés »

En fonction du nombre de bases et du nombre de chevaux associés que l’on détermine, on réduit ainsi de façon importante le nombre de paris joués (mais en acceptant en contrepartie le risque de s’être trompé dans sa sélection).
Ainsi, si sur une course de 16 partants on définit 2 bases et 8 autres chevaux associés, le nombre de paris joués au quinté dans tous les ordres est de A_{5}^2 x A_{8}^3, soit 6 720 paris au lieu des 524 160 initiaux !
Ce nombre de paris reste important, mais peut être réduit si on ne coche pas l’option « dans tous les ordres » lors d’une prise de pari en champ. Dans ce cas on « fixe » les bases, c’est à dire que sur cet exemple, on attribue une place à chacun de nos 2 chevaux de base (par exemple la 1ère place pour notre base 1 et la 2ème place pour notre base 2), et on ne joue que les arrangements de nos chevaux associés sur les 3 places restantes, dans tous les ordres.
Cela donne ici A_{8}^3 soit à présent 336 paris.
C’est ce principe que M. X appliqua lors de son premier pari, avec un résultat concluant.
C’est également le principe de la formule « champ réduit » du PMU, qui permet en un seul pari de jouer tous les paris à partir de bases sélectionnées et de chevaux associés, et ce en pouvant préciser si on souhaite jouer tous les ordres (ce qui a alors pour effet de jouer tous les ordres également pour les bases et pas seulement pour les chevaux associés).
Si on souhaite jouer tous les autres chevaux partants en associés, alors on peut jouer en formule « champ total » pour n’avoir à sélectionner que les bases.
Si on n’a pas de base spécifique à sélectionner, et qu’on ne sélectionne donc que des chevaux associés, alors cela revient à jouer en formule « combiné », ce qui va créer toutes les combinaisons (ou arrangements, si on souhaite jouer dans tous les ordres) de 5 chevaux parmi l’ensemble des chevaux que l’on sélectionne.
Le PMU propose également depuis février 2020 une option de jeu en « champ libre », qui offre encore plus de facilité, en permettant, pour chaque cheval que l’on sélectionne, d’indiquer la ou les places auxquelles on souhaite les jouer. L’ensemble des combinaisons ou arrangements correspondants seront générés et permettront ainsi de les jouer en une seule prise de pari.
On peut de cette manière réduire le nombre de paris et donc la mise totale jouée, augmentant ainsi notre espérance de gain, pourvu que notre estimation des bases et chevaux associés soit juste.
En utilisant l’option « Flexi » du PMU on va pouvoir réduire encore la mise à 25% ou 50% de la mise de base (de 2€ pour un quinté unitaire), et donc jouer plus de paris pour la même somme, le gain potentiel étant bien sûr divisé proportionnellement en cas de victoire.

Le nombre de paris joués peut être encore plus réduit, en utilisant des systèmes réducteurs plus complexes et non fournis par les opérateurs.
Pour comprendre comment ceux-ci fonctionnent vous trouverez ici l’explication du principe de l’outil réducteur que nous avons développé, ainsi qu’un tableau récapitulatif des réductions de paris possibles au quinté, via les systèmes réducteurs des opérateurs et via les systèmes avancés comme celui proposé par notre outil.