SVM

Publié le par

Principe de l’algorithme SVM
L’algorithme SVM (Support Vector Machines) est un algorithme performant de Machine learning pour la classification supervisée, permettant de résoudre des problèmes de classification (mais aussi de régression). L’idée consiste à tracer un hyperplan permettant de séparer nos points, l’hyperplan étant tracé de manière à maximiser la distance de chaque point à l’hyperplan, de sorte que cette frontière soit la plus discriminante possible, et que notre classification soit ainsi la plus pertinente possible.
Ci-dessous un exemple simple en dimension 2 (on considère que nos données sont décrites par seulement 2 features, nos vecteurs sont donc des points dans le plan). L’algorithme va chercher à séparer les points bleus et verts en traçant la droite rouge, qui offre une marge maximale (en jaune) entre les 2 classes:

Les points se trouvant sur les 2 droites formant la marge sont les vecteurs « supports », d’où le nom de l’algorithme.
Pour améliorer sa performance, SVM utilise un paramètre appelé paramètre de coût (C).
Ce paramètre va permettre de relâcher la contrainte d’avoir tous les points en dehors de la marge, en autorisant plus ou moins de points « mal classés » en fonction de la valeur donnée à C, passant ainsi d’un principe de « hard margin » à un principe de « soft margin ».
Cela permet à l’algorithme un arbitrage pour avoir une marge optimale pour un maximum de points bien classés. Avec un paramètre C faible, les points à l’intérieur de la marge sont moins pénalisés qu’avec un paramètre C élevé. A l’extrême, avec un C infini, on n’autorise aucun point à l’intérieur de la marge et on revient à du hard margin.
Cet algorithme s’applique bien pour des données séparables linéairement.
Pour des données non linéairement séparables, il reste possible d’utiliser le « kernel trick » consistant à projeter les données dans un espace de dimension supérieure (via une fonction de mapping spécifique), où la séparation pourrait cette fois être linéaire (un hyperplan existe dans un espace de dimension supérieure et permet de séparer nos données).

Objectif
Nous allons ici chercher à construire un classifieur permettant de séparer nos chevaux en 2 classes:

  • la classe 1 correspondant aux « gagnants » (arrivant à la 1ère place)
  • la classe 0 correspondant aux « non gagnants » (arrivant après la 1ère place)

On considère pour cela les chevaux de façon équivalente, c’est à dire que l’algorithme va tous les prendre en compte en même temps, et les classer en fonction de leurs caractéristiques (décrites par les features), sans prendre en compte le fait que des chevaux courent éventuellement dans une même course. L’algorithme peut donc potentiellement prédire plusieurs gagnants dans une même course, ou à l’inverse aucun gagnant, même si on sait qu’il existera bien un et un seul gagnant pour chaque course (à noter que pour simplifier nous avons exclu du dataset les rares courses avec chevaux gagnants ex-aequo).

Périmètre de données utilisé
Nous décidons de travailler uniquement sur un dataset dans un premier temps, l’idée étant de passer un maximum de temps sur l’exploration des différents algorithmes. Nous choisissons pour commencer le trot attelé, cette discipline étant plus « prédictible » par nature, comme le savent les parieurs, et comme nous avons pu le voir dans nos différentes analyses statiques. Les algorithmes pourront ensuite être appliqués sur d’autres datasets comme celui de plat.
De même, afin de réduire les temps de calcul pour avoir plus de temps à passer sur la méthodologie et le code, nous travaillerons au départ sur un échantillon aléatoire de 10% du dataset soit déjà près de de 27500 chevaux puisque celui-ci est constitué de près de 275 000 chevaux.
Les features utilisées ici sont composées de données numériques et données catégorielles:

  • Les données numériques utilisées sont:
    Numero, Mois, Prix, Nombre de chevaux réel, Nombre de non partants, Distance, Distance supplémentaire, Age, Note de musique, Rapport relatif à 10min, Récence, Note de pronostic.
  • Les données catégorielles utilisées sont:
    Jour, Période, Hippodrome, Type course, Autostart, A réclamer, Sexe, Déferrage.

Traitement des données
Pour pouvoir utiliser SVM, les données doivent être transformées:

  • Les variables numériques doivent être normalisées.
    Nous utilisons pour cela StandardScaler (mais nous aurions aussi pu utiliser un autre scaler comme MinMaxScaler)
  • Les variables catégorielles doivent être encodées
    Nous utilisons pour cela OnehotEncoder. Le principe est pour chaque variable, de créer autant de colonnes (nouveaux features) qu’il y a de valeurs possibles. Chaque valeur devient un feature représentant une classe de la variable d’origine, à laquelle on attribue la valeur 0 ou 1. On démultiplie ainsi le nombre de features, mais les données sont maintenant normées.

En faisant tourner les premiers modèles, nous nous apercevons rapidement que nous obtenons d’excellents taux de bonne classification sur notre dataset, ne serait-qu’avec un simple algorithme de régression linéaire, avant même d’utiliser le SVM: on obtient 93%.
En observant la matrice de confusion, on observe qu’en fait notre modèle est biaisé et prédit toujours la classe 0 ! (chevaux non gagnants).
On est en réalité dans un cas d’underfitting venant de la distribution de nos données.
En effet, on s’aperçoit qu’on a en moyenne dans notre dataset 13 chevaux « non gagnants » pour 1 cheval « gagnant ». Les 93% correspondent bien à 13/14.
Ce phénomène est classique lorsqu’on travaille avec un dataset à classes non équilibrées (unbalanced dataset).

Pour pallier à ce problème et travailler sur des datasets équilibrés, nous explorons 2 méthodes différentes:
1/ nous retravaillons le dataset pour l’équilibrer « manuellement », en réduisant le nombre de « non gagnants » pour qu’il corresponde au nombre de gagnants, et avoir ainsi 50% de gagnants et 50% de non gagnants dans notre dataset.
2/ nous utilisons toujours le même dataset (échantillon de 10% du dataset initial), mais nous demandons à l’algorithme de moduler les poids attachés aux classes 0 (non gagnant) et 1 (gagnant) à l’aide du paramètre class_weights.
Ce paramètre va permettre de moduler différemment le paramètre de coût C (décrit plus haut) en fonction de la classe. Le paramètre C sera ainsi multiplié par 13 pour la classe 1, alors qu’il restera à un coefficient 1 pour la classe 0, autorisant ainsi beaucoup moins de chevaux « gagnants » d’être mal classés (présents dans la marge de l’hyperplan). L’hyperplan sera ainsi tracé de façon plus précise pour mieux séparer gagnants et non gagnants.

Résultats méthode 1 – dataset équilibré à 50-50
Nous présentons ci-dessous les résultats obtenus par cette méthode, pour chaque type de SVM, et en les faisant précéder d’une régression logistique afin d’avoir un point de comparaison pour évaluer les performances de nos modèles SVM.

Avant d'utiliser les différents algorithmes SVM, nous procédons d'abord au test de l'algorithme plus rapide et basique qu'est la régression logistique, afin d'avoir un point de comparaison des performances de nos algorithmes SVM.
La régression logistique est un modèle linéaire généralisé, permettant de modéliser la probabilité d'être dans la classe 0 ou 1, en fonction d'une combinaison linéaire des variables/features décrivant nos vecteurs (les chevaux).
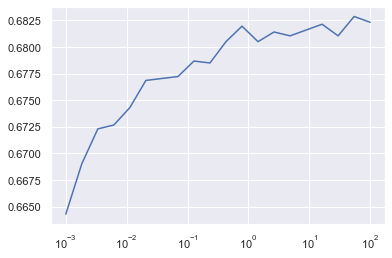
De façon analogue au paramètre de coût C présenté ci-dessus dans le principe de l'algorithme SVM, il existe un paramètre de régularisation C en régression logistique, que nous faisons varier ici pour obtenir le meilleur score (correspondant au taux de bonne classification des chevaux).

Le meilleur score est ici de 0.717 (soit un taux de bonne classification de 71,7% avec cet algorithme sur ce dataset), et est obtenu pour C=0.0207.
On a donc un algorithme plus performant que le hasard (le hasard correspondant à un taux de bonne classification de 50%), mais ce taux reste modeste et justifie que l'on cherche des algorithmes plus performants.

Ici nous utilisons un kernel linéaire, c'est à dire que nous cherchons à séparer les données telles quelles via l'algorithme SVM, avec une séparation effectuée par un hyperplan.
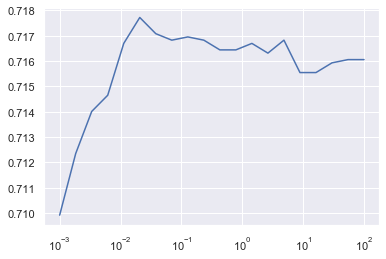
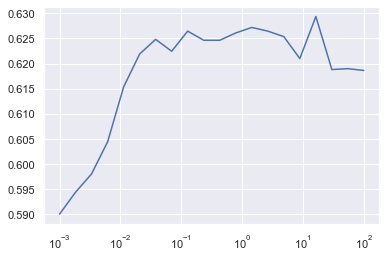
Nous lançons le modèle en faisant varier le paramètre C de 0.001 à 100, pour voir quelle valeur de C permet d'optimiser le score.

Python nous indique que le meilleur score est obtenu pour C=0.0379 environ. Le score est alors de 0,718 ce qui signifie que l'algorithme effectue la bonne classification dans 71,8% des cas. Ce taux est quasiment identique à celui obtenu avec la régression logistique.

L'algorithme SVM poly utilise le kernel trick présenté ci-dessus, pour transformer les données dans un espace de dimension supérieure, via une fonction de mapping polynômiale, et voir si dans cet espace un hyperplan permet de séparer judicieusement les données.
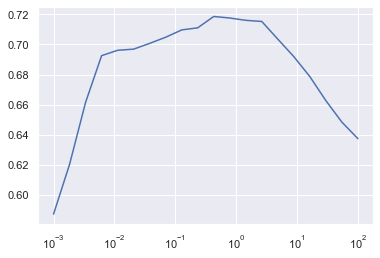
Ici aussi on cherche à optimiser le paramètre C afin de pouvoir comparer le taux de bonne classification avec celui des autres algorithmes, après optimisation selon la même méthode.

On voit ici qu'on trouve le meilleur score pour C=0.428, on a alors à nouveau un taux de bonne classification de 72% environ.

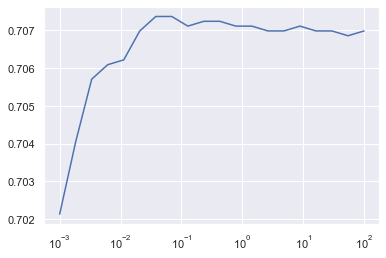
On utilise cette fois le kernel sigmoïde, c'est à dire qu'on transforme cette fois les données dans un espace de dimension supérieure à l'aide de la fonction sigmoïde.

Le meilleur score est obtenu pour C=0.0207, on a alors un taux de bonne classification de 0.705, on reste donc au même niveau de performance que les précédents algorithmes, on fait même légèrement moins bien.

On utilise ici le kernel RBF, c'est à dire qu'on transforme nos données dans un espace de dimension supérieure à l'aide de la Radial Basis Function, qui va permettre de tracer des frontières de décision incurvées.
En plus du paramètre de coût C, un paramètre important lorsqu'on utilise le kernel RBF est le paramètre Gamma, qui va jouer sur la "courbure" de cette frontière. Plus Gamma est élevé, plus la courbure est élevée, permettant ainsi d'encercler les points.
Comme nous avons ici 2 paramètres à optimiser, nous n'utilisons donc pas une courbe pour déterminer le paramètre optimal comme précédemment, mais la fonctionnalité gridsearchCV qui va permettre d'explorer l'ensemble des combinaisons de valeurs entre ces 2 paramètres, parmi une liste de valeurs qu'on fournit pour chacun.
On fournit ici les listes suivantes:
parametres = {'classifier__C':[1,10,20,50,100], 'classifier__gamma':[0.001,0.01,0.1,1,10]}

et on obtient le résultat suivant:

Encore une fois, on retrouve un taux de meilleure classification de 72% environ, obtenu pour C=10 et Gamma=0.01.

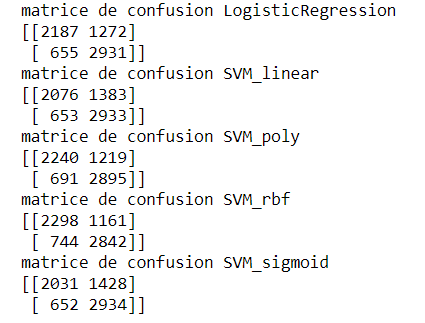
Les matrices de confusion nous permettent de voir comment ont été classés chaque type d'éléments par notre algorithme:
- combien de chevaux de classe 0 (non gagnants) sont classés en classe 0 (non gagnants)
- combien de chevaux de classe 1 (gagnants) sont classés en classe 0 (non gagnants)
- combien de chevaux de classe 0 (non gagnants) sont classés en classe 1 (gagnants)
- combien de chevaux de classe 1 (gagnants) sont classés en classe 1 (gagnants)

Les classes réelles se lisent en lignes et les classes prédites en colonnes:

Ainsi, il faut lire ici, pour le SVM linéaire par exemple:

2076 chevaux de classe 0 (non gagnant) sont prédits à 0 (ce sont les vrais négatifs)
653 chevaux de classe 1 (gagnant) sont prédits à 0 (ce sont les faux négatifs)
1383 chevaux de classe 0 (non gagnant) sont prédits à 1 (ce sont les faux positifs)
2933 chevaux de classe 1 (gagnant) sont prédits à 1 (ce sont les vrais positifs)

A noter qu'on retrouve ici le score de l'algorithme en effectuant le rapport des chevaux bien classés sur le nombre total de chevaux à classer.
Exemple pour le SVM linéaire:
2076+2933/(2076+2933+653+1383)=0.711 (à comparer au 0.718 mentionné précédemment pour SVM linéaire, la légère différence constatée restant toutefois ici à expliquer..)

On voit ici que les algorithmes prédisent bien des chevaux dans chaque classe, nous n'avons donc manifestement pas de problème d'overfitting ou d'underfitting.

Etant ici dans un cas de classification binaire, on utilise la courbe ROC pour afficher le taux de vrais positifs (fraction des gagnants qui sont effectivement prédits gagnants) en fonction du taux de faux positifs (fraction des non gagnants qui sont incorrectement prédits gagnants).
Idéalement la courbe doit monter verticalement sur l'axe des Y jusqu'à Y=1 puis suivre la droite Y=1 jusqu'à X=1.
La performance de la courbe ROC est mesurée par la valeur AUC, qui correspond à l'aire sous la courbe: si la courbe est idéale alors AUC=1, si au contraire elle suit la courbe inverse, alors AUC=0.
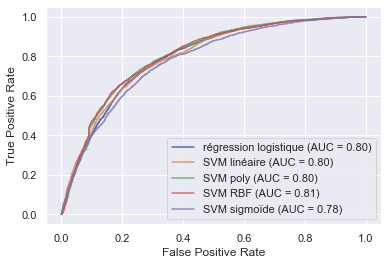
Voyons les courbes ROC de nos différents classifieurs présentés précédemment:

On voit ici que les courbes ROC sont très proches, ce qui est cohérent avec les taux de bonne classification très proches, trouvés aux alentours de 72% pour l'ensemble des algorithmes. Les classifieurs ont donc des performances équivalentes.

On peut conclure de ces tests sur ces différents modèles que l’extrait du dataset composé à 50% de gagnants et 50% de non-gagnants est relativement simple à séparer, les algorithmes plus poussés ne font donc pas mieux que les plus simples. Le taux de bonne classification obtenu est d’environ 72%, ce qui n’est pas excellent mais peut être qualifié de satisfaisant (on fait bien mieux que le hasard qui fourni un taux de 50%).
Cependant, il faut noter que dans la réalité, nous cherchons à classer l’ensemble des chevaux d’une course, nous allons donc présenter au modèle une liste parmi lesquels nous ne voudrons sélectionner qu’un gagnant. Cette liste est donc déséquilibrée par nature, ainsi la méthode 2 présentée ci-dessus (consistant à rééquilibrer les classes), semble pertinente à explorer.

Résultats méthode 2 – dataset modulé avec class_weight
Comme pour la méthode 1, nous présentons ci-dessous les résultats obtenus par cette méthode, pour chaque type de SVM, et en les faisant précéder d’une régression logistique afin d’avoir un point de comparaison pour évaluer les performances de nos modèles SVM..

Comme pour la méthode 1, avant d'utiliser les différents algorithmes SVM, nous procédons d'abord au test de l'algorithme plus rapide et basique qu'est la régression logistique, afin d'avoir un point de comparaison des performances de nos algorithmes SVM.

Le meilleur score est ici de 0.669 (soit un taux de bonne classification de 66,9% avec cet algorithme), et est obtenu pour C=54.56.
On a donc un algorithme plus performant que le hasard (le hasard correspondant à un taux de bonne classification de 50%), mais la performance restant assez faible par rapport à ce qu'on peut espérer.

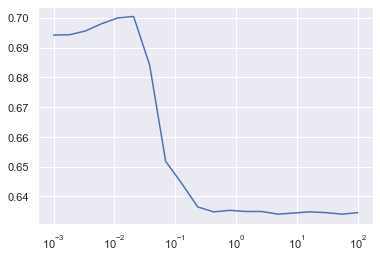
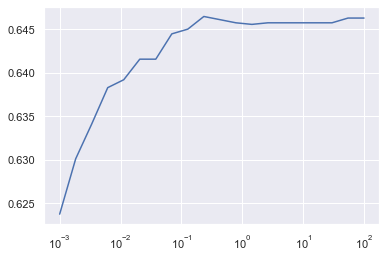
Nous lançons le modèle en faisant varier le paramètre C de 0.001 à 100, pour voir quelle valeur de C permet d'optimiser le score.

Python nous indique que le meilleur score est obtenu pour C=0,234 environ. Le score est alors de 0,646 ce qui signifie que l'algorithme effectue la bonne classification dans 64,6% des cas.
On voit sur la courbe que l'optimisation de C nous fait gagner environ 2% de score, mais le taux obtenu reste modeste, inférieur à celui de la régression logistique.

L'algorithme SVM poly utilise le kernel trick présenté ci-dessus, pour transformer les données dans un espace de dimension supérieure, via une fonction de mapping polynômiale.

On voit ici qu'on trouve le meilleur score pour C=29.76, on a alors un taux de bonne classification de 87% ce qui un taux qu'on peut qualifier de bon.
Il faudra cependant vérifier avec les matrices de confusion et courbes ROC que nous ne sommes ni en underfitting (sous-apprentissage, on n'apprend pas assez des données) ni en overfitting (sur-apprentissage, on apprend les données par coeur).

On utilise cette fois le kernel sigmoïde, c'est à dire qu'on transforme cette fois les données dans un espace de dimension supérieure à l'aide de la fonction sigmoïde.

Le meilleur score est obtenu pour C=16.23, on a alors un taux de bonne classification de 0.63, ce qui est là aussi peu satisfaisant.

Comme vu pour la méthode 1, nous cherchons à optimiser les paramètres C et Gamma à l'aide de gridsearchCV.
On fournit ici les listes suivantes pour le gridsearch:
parametres = {'classifier__C':[0.01,0.1,1,10,100], 'classifier__gamma':[0.001,0.01,0.1,1,10]}

et on obtient le résultat suivant:

Ceci est suspect puisqu'on retrouve le taux de 93% correspondant à un classement systématique dans la classe 0, comme nous l'avons vu plus haut, lorsque nous utilisions le dataset initial, sans rééquilibrage des classes.
Nous pouvons voir dans les onglets "Matrices de confusion" et "Courbes ROC" que l'algorithme est ici en effet en underfitting.

Comme pour la 1ère méthode avec le dataset à 50/50, on affiche ici les matrices de confusion de nos différents algorithmes présentés précédemment:

La matrice de confusion du modèle SVM RBF est ici particulièrement frappante:
on constate que dans le 2ème colonne (correspondant à une classe prédite à 1), on n'a aucun cheval, ce qui signifie que l'algorithme prédit toujours la classe 0, que ce soit pour les chevaux réellement de classe 0 (sur la première ligne), ou bien réellement de classe 1 (sur la deuxième ligne). L'algorithme classe donc systématiquement tous les chevaux en non-gagnants.

Cela met en évidence que l'algorithme SVM avec kernel RBF ne convient pas à notre distribution de données, il n'a pas pu tracer d'hyperplan séparateur même dans un espace de dimension supérieure.

Comme pour la méthode 1 on trace les courbes ROC de nos différents classifieurs pour évaluer leur performance:

On voit que le modèle qui performe le mieux est le SVM poly, qui se rapproche au mieux de la courbe ROC idéale (prédit beaucoup de vrais positifs et presque pas de faux positifs) avec une valeur AUC de 0.93.
Comme on l'a vu on a un taux de bonne classification de 87%, et le modèle n'est pas biaisé puisque comme le montre la matrice de confusion, on prédit aussi bien des gagnants que des non gagnants.
Viennent ensuite la régression logistique et le SVM linéaire (quasiment identiques, liés à des algorithmes similaires).
Comme on l'avait préssenti et déjà vu avec la matrice de confusion, on voit que SVM RBF est un mauvais classifieur bien que son accurary en test soit supérieure (0.93 vs 0.65-0.67 pour régression logistique et SVM linéaire ), car il prédit toujours la classe 0 ! (non gagnant). Sa courbe ROC est en effet caractéristique d'un mauvais classifieur, puisqu'il ne prédit que des faux positifs, il se trompe tout le temps pour le classement des gagnants.

Modèle retenu et utilisation
En conclusion des résultats présentés ci-dessus, nous avons obtenu, avec l’algorithme SVM poly, un classifieur binaire permettant de classer efficacement nos données, avec un score (accuracy) de 87% environ, donc satisfaisant.
L’algorithme prédit bien des gagnants et des non-gagnants, et s’applique sur un dataset correspondant à la réalité, c’est à dire avec des classes déséquilibrées par nature (on a en moyenne 13 fois plus de non gagnants que de gagnants). Plus que l’accuracy c’est cependant la précision qui est importante dans notre problématique, puisqu’elle définit la capacité à bien trouver les chevaux gagnants, et que nous travaillons sur un dataset avec des classes déséquilibrées.
En la calculant à partir de la matrice de confusion de SVM poly, on obtient une precision de
p=359/(359+130)=73%, ce qui reste un taux satisfaisant.

L’algorithme SVM avec kernel polynomial permet de classer de façon performante les chevaux d’un dataset déséquilibré en gagnant ou non gagnant, avec un taux de bonne classification de 87% pour l’ensemble des chevaux, et de 73% pour les chevaux gagnants uniquement.

On peut maintenant tester manuellement notre modèle sur des chevaux du dataset mis de côté lors de la création du jeu d’apprentissage et du jeu de test (présents dans aucun de ces jeux de données), pour réaliser un test sur un nouveau cheval, jamais vu par l’algorithme. On peut alors comparer la classe réelle et la classe prédite:

Il faut cependant noter que si on cherche maintenant à afficher la probabilité que le cheval se trouve dans la classe 0 ou 1, et pas simplement sa classe, on peut être confronté à des contradictions entre la probabilité obtenue et la classe obtenue, comme sur cet exemple:

La classe réelle est 0, l’algorithme s’est ici trompé en prédisant la classe 1, mais ce qui est marquant c’est qu’il fournit une probabilité d’être dans la classe 0 de 88% environ, et d’être dans la classe 1 de 12% environ !
En faisant des recherches dans la documentation Scikit learn on s’aperçoit que ceci est un problème connu de l’algorithme Platt scaling utilisé pour le calcul de la probabilité dans Scikit learn.
Si on souhaite avoir un facteur de confiance sur notre classement, sans qu’on ait besoin d’une réelle probabilité, il est alors conseillé d’utiliser Decision_function qui ne fournit pas une probabilité mais la distance à l’hyperplan, ce qui nous donnera une idée si la classification est « forte » (relativement fiable) ou « faible » (relativement peu fiable) en fonction de la valeur retournée.

Dans le cas d’une classification binaire une seule valeur est retournée, son signe donne la classe (0 si négatif, 1 si positif) et sa valeur absolue la distance du point testé à l’hyperplan.
Il nous faut cependant réapprendre notre modèle SVM poly au préalable, en précisant probability=False lorsqu’on fitte le modèle.
On observe alors systématiquement qu’on a bien une distance à l’hyperplan cohérente avec la classe prédite, comme sur cet exemple, où on prédit la classe 1 (gagnante), et on a bien une distance à l’hyperplan positive (la classe réelle était cependant ici la classe 0):

Pour affiner notre classification et pouvoir comparer 2 chevaux classés gagnants ou 2 chevaux classés non gagnants, on pourra donc utiliser la distance à l’hyperplan.